
The data generated by each scheme is shown in fig, along with the original input. It finds values at intermediate points, of a one-dimensional function that underlies the data. The other schemes we could use are nearest, linear, and spline. The interp1 command interpolates between data points. Examples collapse all Linear Interpolation Using interp1q Generate a coarse sine curve and interpolate over a finer abscissa.
The vector x specifies the coordinates of the underlying interval. Here 'cubic' is the choice for the interpolation scheme. Description example yi interp1q (x,Y,xi) returns the interpolated value of the 1-D function Y at the points of column vector xi. % generate y i at x i with cubic interpolation. Step1: Generate a vector x i containing desired points for interpolation. There are two simple steps contained in interpolation: providing a list (a vector) of points at which you wish to get interpolated data and executing the appropriate function (e.g., interp1) with the desired choice for the method of interpolation. I have checked the datevector and the time values are incrementing every minute. I have used the following commands to re-sample it with constant time increment (60sec increment).
#HELP MATLAB INTERP1 SERIES#
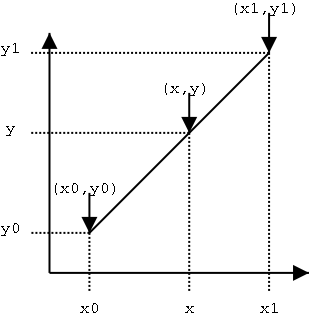
The interpolation is especially useful for periodic functions (i.e., if values of y are periodic). I have a time series matrix that is not evenly spaced in time. This is similar to interp1 except that the data is interpolated first by taking the Fourier Transform of the given data and then calculating the inverse transform using more data points. Cubic splines fit separate cubic polynomials between successive data points by matching the slopes as well as the curvature of each segment at the given data points.įast Fourier Transform (FFT)-based 1-D data interpolation. One-dimensional interpolation that uses cubic splines to find y j at desired x j,given y i at x i. To specify cubic interpolation instead of linear, for example, in interp1, use the syntax: The choice of the method dictates the smoothness of the interpolated data. The choice for the technique is nearest, linear, cubic, or spline. In each function, we have the option of specifying a method of interpolation. Vnew=interp3(x,y,z,xnew,ynew,znew,method).Īlso, there is an n-dimensional analog, interpn, if you ever need it. Given v i at (x i, y i,z i), finds v j at desired(x j,y j,z j). It is called two-dimensional interpolation because z depends on two variables, x, and y. Given z i at (x i, y i), finds z j at desired (x j,y j )from z=f(x,y).The function f is found from interpolation. Where the method is an optional argument discussed after the description of interp2 and interp3. It is called one-dimensional interpolation because y depends on a single variable x. Here f is a continuous function that is seen from interpolation. It finds values of a one-dimensional function f(x) underlying the data at intermediate points. Given y i at x i, finds y j at x j from y j=f(xj ). The interp1 command interpolates between data points. Let us understand these functions of MATLAB one by one: interp1 MATLAB provides the following functions to help interpolation: In MATLAB, we can interpolate our data using splines or Hermite interpolants on a fly. The most common interpolation technique is Linear Interpolation.Ī more exotic interpolation scheme is to link the data points using third degree or cubic polynomials. All the tutorials are completely free.Interpolation is the process of describing a function which "connects the dots" between specified (data) points.
#HELP MATLAB INTERP1 FREE#
This website contains more than 200 free tutorials! Every tutorial is accompanied by a YouTube video.

If we type “help interp1” we can obtain the following options. If we want to perform some other type of interpolation, we need to specify the fourth argument. The MATLAB function “interp1()” computes interpolated values using the default settings that correspond to linear interpolation. In our case, this vector is called “time_dense”. The third argument is a set of values on the x axis at which we want to compute the interpolated values. In our case, the first two arguments are “time_coarse” and “coarse_function” which are used to define the original function values. The first two arguments are the set of points that define the original function. This sample program uses the Matlab Interp1 One-dimensional data interpolation (table lookup) function. The MATLAB function “interp1()” is used to interpolate the function values. Plot(time_coarse,coarse_function,'o',time_dense,dense_function_interpolated,'.') % Vq = interp1(X,V,Xq) interpolates to find Vq, the values of the underlying function V=F(X) at the query points Xq.ĭense_function_interpolated = interp1(time_coarse,coarse_function,time_dense) Coarse_function=time_coarse.^2-0.1*time_coarse.^3


 0 kommentar(er)
0 kommentar(er)
